Vamos continuar resolvendo algumas questões de matemática do ENEM 2014, Caderno Azul. Vamos lá…
Questão 141 Caderno Azul
Nessa questão, é necessário saber o que é mediana. A mediana é uma medida da localização do centro de uma amostra. Para obter a mediana é preciso ordenar os elementos da amostra em ordem crescente, ou seja, do menor para o maior. Se o número de elementos da amostra é ímpar, então a mediana é o elemento do meio. No caso em que o número de elementos é par, então a mediana é a média dos dois mais centrais. Mais um detalhe: não tem problema ter elementos repetidos, você continua ordenando os elementos do menor para o maior. Agora vamos para a questão.
Vamos ordenar as notas do candidato K em ordem crescente: 33, 33, 33, 34. Como o número de elementos é par, então a mediana é a média dos dois mais centrais: ![]() . Agora vamos fazer o mesmo para os demais candidatos:
. Agora vamos fazer o mesmo para os demais candidatos:
Candidato L: 32, 33, 34, 39 ![]()
![]()
Candidato M: 34, 35, 35, 36 ![]()
![]()
Candidato N: 24, 35, 37, 40 ![]()
![]()
Candidato P: 16, 26, 36, 41 ![]()
![]()
Logo, a resposta certa é N. Note que, sabendo o que é mediana, esse exercício também pode ser feito rapidamente.
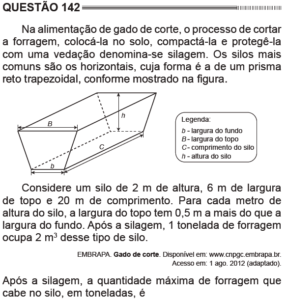
Questão 142 Caderno Azul
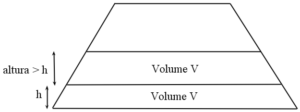
Neste problema temos que calcular o volume do prisma reto trapezoidal. As medidas ![]() ,
, ![]() ,
, ![]() foram dadas. Falta calcular
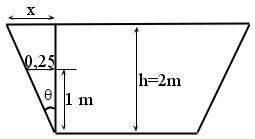
foram dadas. Falta calcular ![]() . Note que é dada ainda a informação de que a cada metro de altura, a largura do topo tem 0,5 m a mais. Logo, dá para calcular o ângulo
. Note que é dada ainda a informação de que a cada metro de altura, a largura do topo tem 0,5 m a mais. Logo, dá para calcular o ângulo ![]() do trapézio como mostrado na figura abaixo:
do trapézio como mostrado na figura abaixo:
Note que ![]() . Contudo, não é necessário calcular o valor de
. Contudo, não é necessário calcular o valor de ![]() , uma vez que
, uma vez que ![]() . Portanto,
. Portanto,
![]()
Agora, temos o valor de ![]() ,
, ![]() . Com o valor de
. Com o valor de ![]() podemos calcular a área do trapézio da figura acima:
podemos calcular a área do trapézio da figura acima:
![]()
O volume do prisma será ![]() . Como, de acordo com o enunciado, 1 tonelada ocupa
. Como, de acordo com o enunciado, 1 tonelada ocupa ![]() , então temos que a forragem ocupa
, então temos que a forragem ocupa ![]() toneladas por
toneladas por ![]() . Assim, em
. Assim, em ![]() temos
temos ![]() toneladas. A resposta certa é A.
toneladas. A resposta certa é A.
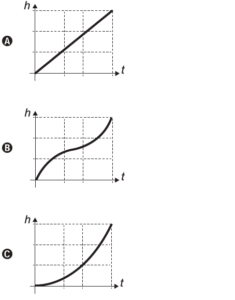
Questão 143 Caderno Azul
Esse dá para fazer sem conta alguma. Vamos primeiro dividir o objeto em três partes: um tronco de cone na parte mais baixa, um cilindro no meio e um outro tronco de cone na parte mais alta. No tronco de cone inferior, a área da base é maior do que a área do topo, isto é, a área da seção do tronco de cone vai diminuindo gradativamente à medida que nos aproximamos do seu topo. Vamos agora supor um primeiro intervalo de tempo ![]() em que a água entra no objeto. Supondo uma vazão constante
em que a água entra no objeto. Supondo uma vazão constante ![]() , então o volume de água que entrou no objeto após
, então o volume de água que entrou no objeto após ![]() segundos é
segundos é ![]() . Considere agora o tronco de cone de volume
. Considere agora o tronco de cone de volume ![]() preenchido após o primeiro intervalo de
preenchido após o primeiro intervalo de ![]() segundos, e denote por
segundos, e denote por ![]() a altura desse tronco de cone, como mostrado na figura abaixo:
a altura desse tronco de cone, como mostrado na figura abaixo:
Vamos considerar agora um segundo intervalo de tempo ![]() . Como a parte não preenchida do objeto tem seções com áreas menores do que a que já foi preenchida, então para ocupar o mesmo volume a altura do novo tronco de cone preenchido após o segundo intervalo de tempo
. Como a parte não preenchida do objeto tem seções com áreas menores do que a que já foi preenchida, então para ocupar o mesmo volume a altura do novo tronco de cone preenchido após o segundo intervalo de tempo ![]() terá que ser maior do que
terá que ser maior do que ![]() , ou seja, a altura após dois intervalos de tempo
, ou seja, a altura após dois intervalos de tempo ![]() é maior do que
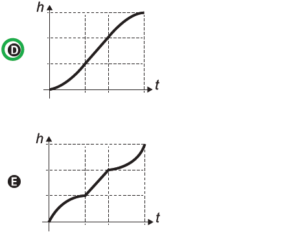
é maior do que ![]() . Note que esse comportamento da altura é condizente somente com as figuras C e D. Para tirar a dúvida entre essas duas, note que na parte do cilindro, como a área da seção é constante e o volume
. Note que esse comportamento da altura é condizente somente com as figuras C e D. Para tirar a dúvida entre essas duas, note que na parte do cilindro, como a área da seção é constante e o volume ![]() de água que entra no objeto após
de água que entra no objeto após ![]() segundos é constante, temos uma variação de altura pelo tempo também constante, o que mostra que a resposta certa é a letra D.
segundos é constante, temos uma variação de altura pelo tempo também constante, o que mostra que a resposta certa é a letra D.
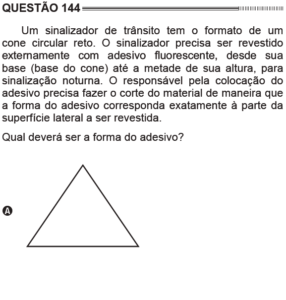
Questão 144 Caderno Azul
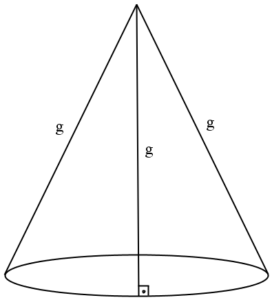
Essa também dá para fazer rápido. A questão tem a ver com a planificação de um cone. Pense em um cone feito de papel. Se pegarmos esse cone e abrirmos ele, qual será o formato encontrado da folha de papel? Essa é a pergunta chave para resolver a questão. Para ver a resposta, considere um segmento de reta qualquer no cone indo do topo até alcançar a base perpendicularmente como mostrado na figura a seguir. Vamos denotar o comprimento desse segmento de reta por ![]() .
.
Note que todos os segmentos de reta do topo até alcançarem a base perpendicularmente terão o mesmo comprimento ![]() . Logo, um cone completo planificado tem a forma apresentado em azul na figura abaixo:
. Logo, um cone completo planificado tem a forma apresentado em azul na figura abaixo:
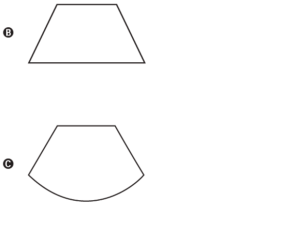
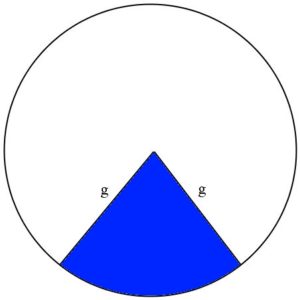 Note que a lateral do cone planificada é um setor circular de raio
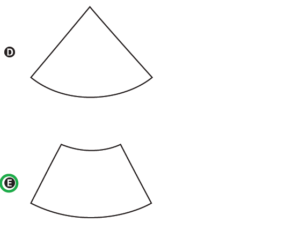
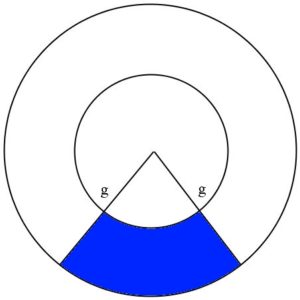
Note que a lateral do cone planificada é um setor circular de raio ![]() . Contudo, essa não é a resposta da questão porque o adesivo será utilizado para revestir apenas a parte inferior do cone, ou seja, da base até a metade de sua altura. Logo, o adesivo deve ter a forma em azul abaixo.
. Contudo, essa não é a resposta da questão porque o adesivo será utilizado para revestir apenas a parte inferior do cone, ou seja, da base até a metade de sua altura. Logo, o adesivo deve ter a forma em azul abaixo.
Questão 145 Caderno Azul
A maneira mais elegante de resolver essa questão é por Álgebra Linear, mas é possível resolver só observando alguns fatos. Primeiro vamos eliminar as letras que não podem estar corretas. Note que a letra D não pode estar correta pois é dito que ![]() quando
quando ![]() . A letra E também não pode ser correta porque
. A letra E também não pode ser correta porque ![]() quando
quando ![]() . Restam A, B e C e aí é só substituir os valores de
. Restam A, B e C e aí é só substituir os valores de ![]() e verificar se dá o
e verificar se dá o ![]() desejado. Logo de cara, testando a letra A, vemos que:
desejado. Logo de cara, testando a letra A, vemos que:
para ![]()
![]()
![]() e
e
para ![]()
![]()
![]()
Resposta correta letra A.