Dicas de matemática com resolução de questões do ENEM - 1

freeimages.com/John evans

Pessoal, vamos postar algumas dicas a partir de hoje para as provas do ENEM. Essas dicas visam ajudar vocês para fazer o exame de maneira mais fácil. Neste post vamos falar de questões de matemática.

Antes de mais nada notem que no ENEM tem muitas questões para serem feitas em pouco tempo. Logo, se quem preparou as questões não enlouqueceu e quer mais é que ninguém consiga fazer as provas, essas questões têm como ser feitas de forma rápida. De fato, elas podem sim e algumas são bem simples. Leia atentamente as questões de forma a entender claramente o enunciado. Na maioria das vezes, a dúvida está no enunciado e não exatamente em como fazer a questão. No ENEM os enunciados são grandes e como o tempo é curto, bate o nervosismo e não se entende direito o enunciado. Vale mais a pena perder tempo lendo direito a questão do que errar algo que você sabe fazer. Vamos mostrar a seguir algumas questões do ENEM 2014 e as suas resoluções.

Questão 136 Caderno Azul

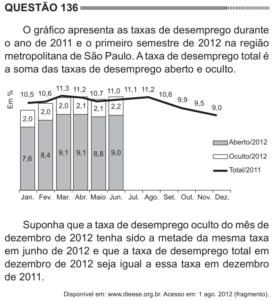
Essa questão requer apenas atenção ao gráfico e ao que é dito, ou seja, requer uma leitura cuidadosa do enunciado e calma. A solução é simplesmente uma divisão e uma subtração. Note que é dito que a taxa de desemprego oculto do mês de dezembro de 2012 é metade da mesma taxa de junho de 2012. Se você observar no gráfico, de acordo com a legenda na parte da direita, o retângulo não preenchido (o retângulo branco) significa essa taxa. Em junho de 2012 o valor da taxa de desemprego oculto era 2,2%. Portanto, em dezembro de 2012 era 1,1% (metade da taxa de junho/2012). Depois é dito que a taxa de desemprego em dezembro de 2012 (TOTAL) é igual à taxa em dezembro de 2011. Novamente, de acordo com a legenda a linha contínua representa os valores totais das taxas de 2011.

Em dezembro de 2011 a linha contínua informa que a taxa TOTAL era 9%. Logo, como a taxa de desemprego OCULTO é 1,1% e a TOTAL é 9%, então a taxa de desemprego ABERTO é 9-1,1=7,9%.

Questão 137 Caderno Azul

Essa é uma questão de porcentagem. Note que é suposto que a variação PERCENTUAL relativa na taxa de fecundidade no período de 2000 a 2010 se repete no período de 2010 a 2020. Logo temos que calcular qual é essa variação percentual. A taxa de fecundidade variou no período de 2000 a 2010 de 2,38 a 1,9, ou seja, variou $2,38-1,9=0,48$ . Portanto, percentualmente, com relação ao ano de 2000, variou $\frac{0,48}{2,38}\times 100\%$ .

Queremos saber a taxa de fecundidade em 2020. Para tanto, vamos calcular a variação na taxa de fecundidade de 2010 a 2020. Como as variações percentuais de 2000 a 2010 e de 2010 a 2020 são iguais temos:

$\frac{\Delta x}{1,9} = \frac{0,48}{2,38}$

em que $\Delta x$ denota o valor da variação na taxa de fecundidade no período de 2010 a 2020. Fazendo as contas:

$\Delta x = \frac{1,9 \times 0,48}{2,38} \approx 0,38$

Logo, o valor da taxa de fecundidade em 2020 será $1,9-0,38 = 1,52$ .

Questão 138 Caderno Azul

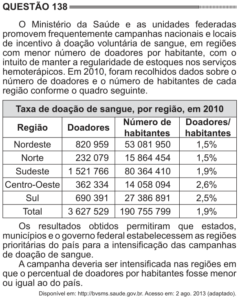
Essa é quase uma questão de português. Note que o texto é enorme e a única coisa que se pede é saber quais regiões do país possuem percentual de doadores por habitantes menor ou igual ao do país.

O total, ou seja, do país, é de $1,9\%$ . Basta observar que as regiões Nordeste, Norte e Sudeste são as que têm percentual de doadores por habitantes menores ou iguais ao total $1,9\%$ . Note que é possível resolver essa questão em menos de dois minutos, basta lê-la com atenção.

Questão 139 Caderno Azul

Essa é uma questão que envolve o conhecimento de fração e área. Note que o carpinteiro quer manter a quantidade de madeira para fabricar uma porta, aumentando a sua altura em $\frac{1}{8}$ . Logo, se a altura da porta era $h$ , agora com o aumento passa a ser $h+ \frac{1}{8} \times h = \frac{9}{8} \times h$ . Como a espessura da porta não muda, então para ter a mesma quantidade de madeira na nova porta, as áreas (largura vezes altura) da nova porta e da porta antiga têm que ser iguais. Seja $l$ a largura da porta antiga. A pergunta é quanto vale a largura da nova porta. A conta é feita pela igualdade das áreas. Vamos chamar de $y$ a largura da nova porta. Então:

$\frac{9}{8} h \times y = h \times l$

Dividindo ambos os lados por $h$ temos:

$\frac{9}{8} \times y = l$

o que mostra que:

$y =\frac{8}{9} \times l$

Logo a resposta correta é $\frac{8}{9}$ .

Questão 140 Caderno Azul

Mais uma questão de porcentagem. Basta ver a redução no consumo para cada atividade apresentada na tabela. Note que ”tomar banho”, ”lavar as mãos” e ”escovar os dentes” juntos na tabela somam $24+3,2+2,4 = 29,6$ litros. De acordo com a ONU, atualmente $25\%$ de 200 litros é a quantidade de água utilizada para as três atividades, ou seja, atualmente gasta-se nas três atividades $\frac{25}{100}\times 200 = 50$ litros. A redução nas três atividades é, portanto,

$50 - 29,6 = 20,4 \text{ litros}$

Falta agora ver a redução nas atividades “dar descarga” e “beber e cozinhar”. O consumo sugerido para dar descarga é de 18 litros e o que é gasto atualmente é $33 \%$ de 200 litros, ou seja, $\frac{33}{100}\times 200 = 66$ litros. A redução então na atividade dar descarga é de

$66-18 = 48 \text{ litros}$

Por fim, na atividade beber e cozinhar é sugerido o gasto de $22$ litros, enquanto que o usado atualmente é de $27 \%$ de 200 litros, isto é, $\frac{27}{100}\times 200 = 54$ litros. A redução nesse caso é de