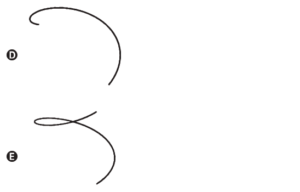Pessoal, mais 10 questões comentadas do ENEM 2014 Caderno Azul, questões 156 a 165. Vamos lá, força…
Questão 156 Caderno Azul
Esse é simples. Dá para fazer rapidinho. Se a escala é 1:100 então 1 cm no projeto equivale a 100 cm na realidade. As dimensões no projeto são 3 cm, 1 cm, e 2 cm. Logo, na realidade são 300 cm, 100 cm e 200 cm. Multiplicando as três dimensões temos o resultado em ![]() :
: ![]() .
.
Questão 157 Caderno Azul
Mais uma vez vem um exercício de média, mediana e moda. Esses conceitos são simples e costumam cair no ENEM. Média é a soma dos elementos de uma amostra dividida pelo número de elementos. A moda é o elemento que mais aparece na amostra. A mediana é o valor que divide a amostra (ordenada do menor para o maior valor) na metade. Quando o número de elementos é par, a mediana é a média dos dois elementos mais centrais, e quando é ímpar a mediana é o elemento do meio (não se esqueça de ordenar primeiro os elementos da amostra do menor para o maior para depois calcular a mediana).
Se a cor branca é a que recebeu número 0 e a cor preta recebeu número 1, e a média dos sapatos que receberam mais reclamações foi 0,45, isto significa que reclamaram mais dos sapatos brancos (média inferior a 0,5). Além disso, a moda representa o valor que mais apareceu. Se a ideia é não vender mais o número que mais apareceu nas reclamações, então temos que olhar a moda. Nesse caso, o 38 não será mais vendido e a resposta certa é a letra A.
Questão 158 Caderno Azul
Essa é de probabilidade. A probabilidade de ser POSITIVO dado que o paciente está com a doença. Temos que ver então quantas vezes deu positivo quando o paciente estava com a doença e dividir pelo número de pessoas doentes. O número de pessoas doentes é a soma da primeira coluna da tabela: 100. Deu positivo 95 vezes, logo a resposta é ![]() .
.
Probabilidade é outro assunto que cai muito em ENEM, mas normalmente sem muita complexidade. É importante ter bastante atenção à pergunta.
Questão 159 Caderno Azul
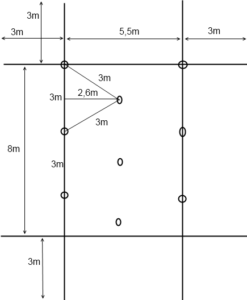
Para plantar as árvores é necessário dar um espaçamento entre as mudas de 3 metros e entre as mudas e os muros também de 3 metros. Além disso, as mudas serão plantadas em filas paralelas ao lado de maior comprimento. Para resolver essa basta ver que em 14 metros dando um espaçamento de 3 metros entre os muros e as mudas e entre mudas, cabem só três mudas em uma fileira, como mostra a figura abaixo:
Obviamente, cabe mais uma fileira igual de 3 mudas porque a outra lateral tem 11,5 metros. Já sei que cabem 6 mudas. A pergunta é então será que cabe mais uma fileira? E de quantas mudas? Vamos então colocar uma muda a três metros de duas na primeira fila, fazendo um triângulo cujos lados têm 3 metros. Esse triângulo é equilátero e a altura dele vai valer
![]()
em que ![]() é o tamanho de um lado do triângulo. No caso em questão
é o tamanho de um lado do triângulo. No caso em questão ![]() e a altura é
e a altura é ![]() , ou seja, a distância entre duas fileiras de mudas pode ser 2,6 m. Então, como há 11,5 metros de largura no terreno, sendo 5,5 m disponíveis para plantar, então dá para colocar três fileiras espaçadas de 2,6 metros, sendo que cada uma tem 3 mudas. Logo, a resposta certa é 9.
, ou seja, a distância entre duas fileiras de mudas pode ser 2,6 m. Então, como há 11,5 metros de largura no terreno, sendo 5,5 m disponíveis para plantar, então dá para colocar três fileiras espaçadas de 2,6 metros, sendo que cada uma tem 3 mudas. Logo, a resposta certa é 9.
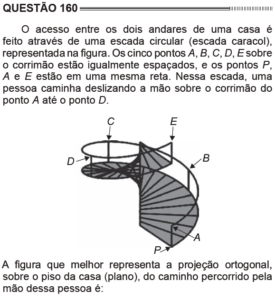
Questão 160 Caderno Azul
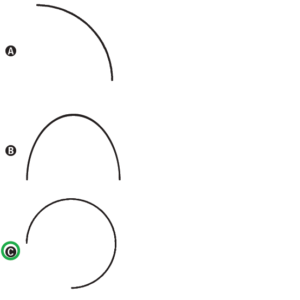
Essa é de projeção ortogonal e o ponto chave da questão está no fato de que os pontos PAE estão sobre uma mesma reta, ou seja, quando projetados os três caem sobre o mesmo ponto. Além disso, note que a escada é circular, logo a sua projeção forma uma circunferência. Note ainda que a circunferência é quase fechada percorrendo-se os pontos ABCD. A única figura que corresponde a parte de uma circunferência quase fechada é a letra C.
Questão 161 Caderno Azul
De novo cálculo de média. Tem que calcular a média de cada reagente e ver quantos experimentos deram resultado acima da média. A média de cada reagente é dada a seguir:
Reagente 1: ![]()
Reagente 2: ![]()
Reagente 3: ![]()
Reagente 4: ![]()
Reagente 5: ![]()
Agora basta ver quantos experimentos para cada reagente estão acima da média:
Reagente 1: 1
Reagente 2: 4
Reagente 3: 3
Reagente 4: 3
Reagente 5: 3
Resposta: letra B
Questão 162 Caderno Azul
Cuidado que essa questão tem uma pegadinha. Primeiro tem que calcular quanto é o valor atual da conta. De acordo com a expressão dada a conta é de: ![]() reais. Como o objetivo é reduzir
reais. Como o objetivo é reduzir ![]() desse valor, então a conta vai para
desse valor, então a conta vai para ![]() reais. Agora temos que calcular qual é o consumo mensal que dá esse valor. Se diminuirmos 4,50 de Cosip, teremos 67,50 reais e o consumo é de 134,10 kWh. Contudo, nessa faixa de consumo a Cosip é de 3,00 e não 4,50. Logo, o valor calculado não está correto e devemos diminuir 3,00 dos 71,55 de conta. Isso dá 68,55 reais, o que corresponde a um consumo mensal de 137,1 kWh que é a resposta certa.
reais. Agora temos que calcular qual é o consumo mensal que dá esse valor. Se diminuirmos 4,50 de Cosip, teremos 67,50 reais e o consumo é de 134,10 kWh. Contudo, nessa faixa de consumo a Cosip é de 3,00 e não 4,50. Logo, o valor calculado não está correto e devemos diminuir 3,00 dos 71,55 de conta. Isso dá 68,55 reais, o que corresponde a um consumo mensal de 137,1 kWh que é a resposta certa.
Questão 163 Caderno Azul
Análise combinatória. Tava faltando uma disso. Vamos lá. Note que o importante é que o cliente veja 8 filmes de ação, 5 de comédia e 3 de drama, que ele pode escolher assistir, entre os filmes do mesmo gênero, na ordem que quiser. Se ele obrigatoriamente tem que ver os 8 filmes de ação, mas poderia ver em qualquer ordem, então estamos falando de permutação. O mesmo vale para os de comédia e os de drama. A permutação de 8 elementos retorna ![]() possibilidades. Para uma mesma ordem de ação escolhida existem
possibilidades. Para uma mesma ordem de ação escolhida existem ![]() possibilidades de comédia e
possibilidades de comédia e ![]() de drama. Logo, o resultado é o produto de todas as possibilidades
de drama. Logo, o resultado é o produto de todas as possibilidades ![]() .
.
Questão 164 Caderno Azul
Mais uma de probabilidade. Se o teste termina na quinta pergunta, é porque a quinta foi errada. Logo, a probabilidade do teste terminar na quinta pergunta é a probabilidade de uma das quatro primeiras estar errada e todas as outras certas e da quinta ser errada. Como a probabilidade de uma resposta estar errada é de 0,2, então, por exemplo, a probabilidade da primeira estar errada e as outras três certas é de ![]() . Contudo, existem 4 possibilidades para as quatro primeiras resposta, pois a errada pode ser a primeira resposta, ou a segunda, ou a terceira ou ainda a quarta. Logo, a probabilidade de uma das quatro primeiras estar errada e as outras certas é
. Contudo, existem 4 possibilidades para as quatro primeiras resposta, pois a errada pode ser a primeira resposta, ou a segunda, ou a terceira ou ainda a quarta. Logo, a probabilidade de uma das quatro primeiras estar errada e as outras certas é ![]() . Por fim, tem ainda que multiplicar pela probabilidade da quinta ser errada que vai dar
. Por fim, tem ainda que multiplicar pela probabilidade da quinta ser errada que vai dar ![]() .
.
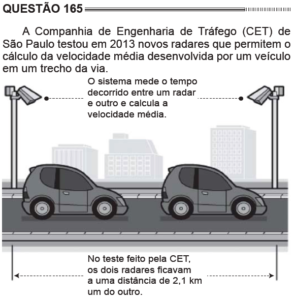
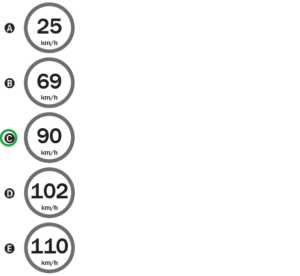
Questão 165 Caderno Azul
A distância entre os dois radares é de 2,1 km e o tempo para percorrer essa distância é de no mínimo 1 minuto e 24 segundos, ou seja, 84 segundos. Só que as placas não estão em km/s e sim km/h. logo, temos que converter segundos para horas. Sabemos que 1 hora tem 3600 segundos. Logo, a conta em km/h é feita da seguinte forma: ![]() km/h.
km/h.