Pessoal, vamos trabalhar agora as questões de matemática 166 a 180 do ENEM 2014 Caderno Azul. Assim, fechamos nossa série de posts de dicas de matemática com resolução das questões do ENEM 2014. Note que os assuntos das questões são variados, mas não são muito complexos. Se você tem um bom conhecimento básico é capaz de fazer a maioria das questões de forma rápida. Vamos lá…
Questão 166 Caderno Azul
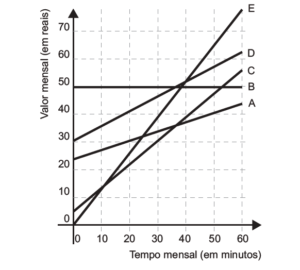
Essa é uma questão de análise de gráfico. Basta olhar no gráfico qual dos planos fornece maior tempo mensal para um valor de 30,00 reais. O plano que está mais à direita no valor de 30,00 reais entre todos os planos é o C, que atinge tempo mensal de 30 minutos.
Questão 167 Caderno Azul
Para resolver essa tem que saber o volume da esfera e do cilindro. O volume da esfera é ![]() e do cilindro é
e do cilindro é ![]() , em que
, em que ![]() denota o comprimento. O volume do comprimido para um raio de 5 mm e considerando
denota o comprimento. O volume do comprimido para um raio de 5 mm e considerando ![]() igual a 3 é a soma do volume do cilindro com os volumes das duas semiesferas:
igual a 3 é a soma do volume do cilindro com os volumes das duas semiesferas: ![]() . Quando o raio é diminuído para 4 mm, obtém-se um novo volume para o comprimido:
. Quando o raio é diminuído para 4 mm, obtém-se um novo volume para o comprimido: ![]() . Logo, a diferença é
. Logo, a diferença é ![]() .
.
Questão 168 Caderno Azul
Mais uma de porcentagem. É um dos assuntos preferidos… Basta dividir a área para agricultura de 80 milhões pela área total 853 milhões e multiplicar por 100. O resultado dá aproximadamente ![]() .
.
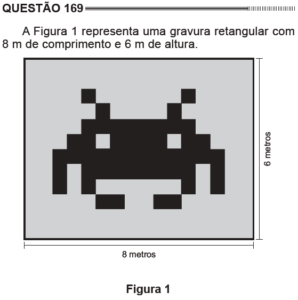
Questão 169 Caderno Azul
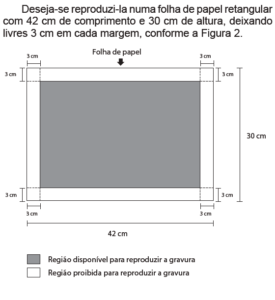
As dimensões disponíveis na figura para reprodução são ![]() e
e ![]() e a figura original tem dimensões
e a figura original tem dimensões ![]() e
e ![]() e devemos manter as suas proporções. Note ainda que as relações entre os lados das figuras são
e devemos manter as suas proporções. Note ainda que as relações entre os lados das figuras são ![]() e
e ![]() , que é menor que
, que é menor que ![]() . Logo, para manter a proporção
. Logo, para manter a proporção ![]() da figura, basta ajustar a escala de acordo com o lado de menor dimensão, ou seja, a escala deverá ser de 1 para
da figura, basta ajustar a escala de acordo com o lado de menor dimensão, ou seja, a escala deverá ser de 1 para ![]() .
.
Questão 170 Caderno Azul
Para essa basta saber o perímetro de uma circunferência. A fórmula é: ![]() ou
ou ![]() . Como são 5 voltas então a solução será
. Como são 5 voltas então a solução será ![]() .
.
Questão 171 Caderno Azul
Novamente mais uma de porcentagem. Note que ![]() de 12t é
de 12t é ![]() t. Essa é a carga central. Como a única resposta que tem 7,2 no centro é a letra C, já sabemos a resposta.
t. Essa é a carga central. Como a única resposta que tem 7,2 no centro é a letra C, já sabemos a resposta.
Questão 172 Caderno Azul
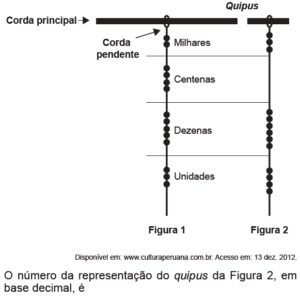
Essa quase não tem o que pensar. A representação é de 3 nós na parte dos milhares, nenhum nó nas centenas, 6 nós nas dezenas e 4 nós nas unidades, ou seja, 3064.
Questão 173 Caderno Azul
Nesta questão tem que saber quanto é um hectômetro em metros. Um hectômetro equivale a 100 metros. Logo, um hectômetro quadrado vale ![]() metros quadrados. Assim, 8 hectômetros quadrados são 80.000 metros quadrados.
metros quadrados. Assim, 8 hectômetros quadrados são 80.000 metros quadrados.
Questão 174 Caderno Azul
Ao todo são 16 galões de 4 litros cada, ou seja, são 64 litros. Como são 10 escolas, cada escola receberá 6,4 litros. Dividindo esse valor por 20 obtém-se 0,320 litro em cada recipiente.
Questão 175 Caderno Azul
Note que o vidro tem transparência no intervalo de ![]() a
a ![]() e esses vidros receberão uma película cuja transparência estará entre
e esses vidros receberão uma película cuja transparência estará entre ![]() e
e ![]() . Logo, o intervalo das porcentagens será de
. Logo, o intervalo das porcentagens será de ![]() de
de ![]() , ou seja
, ou seja ![]() , a
, a ![]() de
de ![]() , ou seja
, ou seja ![]() .
.
Questão 176 Caderno Azul
Essa é simples também. Basta ler com calma o enunciado. Temos que somar o número de bactérias das espécies I e II em cada dia da semana. Somando obtemos 1900 bactérias na terça que é o maior valor.
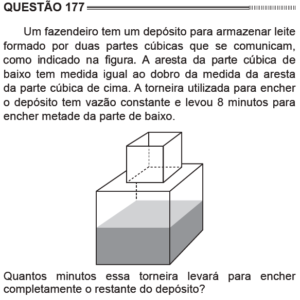
Questão 177 Caderno Azul
Essa tem que saber o volume de um cubo. Observe que os objetos que aparecem no ENEM têm formas normalmente simples. O volume de um cubo é igual a ![]() em que
em que ![]() é o comprimento da aresta. A torneira levou 8 minutos para encher metade do cubo de baixo, ou seja, levaria 16 minutos para enchê-lo todo. A aresta do cubo de cima é metade do cubo de baixo, logo o volume do cubo de cima é
é o comprimento da aresta. A torneira levou 8 minutos para encher metade do cubo de baixo, ou seja, levaria 16 minutos para enchê-lo todo. A aresta do cubo de cima é metade do cubo de baixo, logo o volume do cubo de cima é ![]() . Como o volume a ser preenchido do cubo de cima é menor que do cubo de baixo, então ele enche mais rápido. Essa questão é de regra de três:
. Como o volume a ser preenchido do cubo de cima é menor que do cubo de baixo, então ele enche mais rápido. Essa questão é de regra de três:
![Rendered by QuickLaTeX.com \[\begin{array}{l}& & A^3 \text{ ....................... } 16 \text{ } min \\[-0.6cm] & & \frac{A^3}{8} \text{ ....................... } x \text{ } min \end{array}\]](https://vidaestudantil.com/wp-content/ql-cache/quicklatex.com-bb1b2716ff3a12a1a5706074f5f9e15f_l3.png)
![]()
![]()
Assim, o resultado será 8 minutos para encher metade do cubo de baixo mais 2 minutos para o cubo de cima, ou seja, 10 minutos.
Questão 178 Caderno Azul
A dimensão de uma célula retangular é 6 cm por 8 cm. logo, cada célula possui de diagonal ![]() cm. Portanto, cada célula produz
cm. Portanto, cada célula produz ![]() Wh. Dividindo 20.160 por 240 obtém-se 84, ou seja, são necessárias somente 84 células. Devem ser retiradas então
Wh. Dividindo 20.160 por 240 obtém-se 84, ou seja, são necessárias somente 84 células. Devem ser retiradas então ![]() células.
células.
Questão 179 Caderno Azul
Vamos colocar o texto na forma de uma equação. Antes ele comprava x unidades do produto a 10,00 reais cada e sobrava 6,00 reais. Logo, ele levava ![]() . Se o produto custava 10,00 reais e aumentou
. Se o produto custava 10,00 reais e aumentou ![]() , passou a custar 12,00 reais. Agora ele compra duas unidades a menos, ou seja,
, passou a custar 12,00 reais. Agora ele compra duas unidades a menos, ou seja, ![]() e não sobra nada, isto é, o valor que ele leva é
e não sobra nada, isto é, o valor que ele leva é ![]() . Portanto,
. Portanto, ![]() . Desenvolvendo a equação obtemos:
. Desenvolvendo a equação obtemos:
![]()
Logo, ele leva ![]() .
.
Questão 180 Caderno Azul
Se o voo dura 6 horas e ele sai de A às 15h e chega em B às 18h, então o fuso é de 3 horas. Se ele tem que sair de B e chegar em A às 13h, tem que sair de A ![]() horas antes, ou seja, 4h.
horas antes, ou seja, 4h.