freeimages.com/John evans
Pessoal, mais cinco questões do ENEM 2014, caderno azul.
Questão 151 Caderno Azul
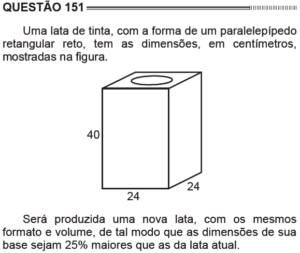
O volume do paralelepípedo é 
. Com um aumento das dimensões da base em 
, passamos a ter largura e comprimento da lata 
. Queremos saber a nova altura 
da lata de forma que o volume permaneça constante. Logo, a conta é 
. Portanto, 
. A redução então na altura foi 
, que percentualmente significa uma redução de 
.
Questão 152 Caderno Azul
Mais uma questão de porcentagem. Cai muita questão desse tipo, o que é bom porque dá para fazer rápido. Note que 8 bilhões de esgoto SEM tratamento são lançados todos os dias e que 
do esgoto TOTAL lançado é COM tratamento. Logo, 8 bilhões de esgoto SEM tratamento correspondem a 
do esgoto lançado. Portanto, chamando de 
a quantidade de esgoto TOTAL lançado temos que 
, o que implica que 
bilhões de litros. Se for reduzida a quantidade de esgoto NÃO TRATADO para 
bilhões e mantida a quantidade total de 
, então a quantidade de esgoto TRATADO passará a ser 
bilhões que percentualmente representam 
.
Questão 153 Caderno Azul
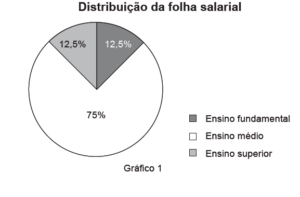
As informações importantes aqui são o gasto com a folha de pagamento 
, a distribuição da folha de acordo com o grau de instrução do funcionário e as quantidades de funcionários.
Como 
da folha são para os funcionários de nível superior, então 
são para pagar os funcionários com ensino superior. Como em 2013 havia 10 funcionários, então o gasto por funcionário com nível superior era de 
.
Como 
da folha são para os funcionários de nível médio, então 
são para pagar os funcionários com ensino médio. Como em 2013 havia 150 funcionários com nível médio, então o gasto por funcionário com nível médio era de 
.
Como da folha são para os funcionários de nível fundamental, então são para pagar os funcionários com ensino fundamental. Como em 2013 havia 50 funcionários então o gasto por funcionário com nível fundamental era de 
.
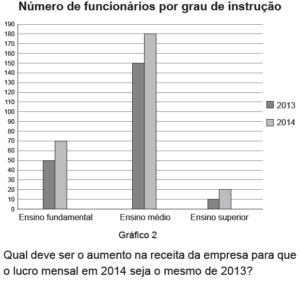
Agora, sabendo o gasto por funcionário em cada um dos níveis de escolaridade, basta multiplicar o gasto por funcionário pelo número de funcionários em 2014 e somar tudo ao final.
O gasto em 2014 com funcionário será:
Ensino Superior: 20 funcionários 
5.000 = 100.000
Ensino Médio: 180 funcionários 2.000 = 360.000
Ensino Fundamental: 70 funcionários 1.000 = 70.000
A soma é 
, o que significa um aumenta com gastos com funcionários de 
. Resposta letra B.
Questão 154 Caderno Azul
Basta dividir o número de vezes que o jogador derrubou todos os pinos pelo número de jogadas de cada jogador. O melhor desempenho é o maior valor.
Jogador 1: 
Jogador 2: 
Jogador 3: 
Jogador 4: 
Jogador 5: 
Comparando os valores podemos ver que o Jogador 4 possui melhor resultado.
Questão 155 Caderno Azul
Neste problema é necessário obter primeiro a média ponderada dos candidatos I e III:
Candidato I: 
Candidato III: 
Portanto, para que o candidato II vença, a sua média deverá ser MAIOR que 21,8.
Candidato III: 
.
Portanto, a solução será 
.