Vamos continuar com as resoluções das questões de matemática do ENEM 2014, Caderno Azul.
Questão 146 Caderno Azul
Este exercício tem umas pegadinhas e você tem que ficar atento. Aqui é dito que ![]() é múltiplo de 10 e não é de 7. Isso não tem a menor importância para resolver a questão. Além disso, é pedido o número de divisores de
é múltiplo de 10 e não é de 7. Isso não tem a menor importância para resolver a questão. Além disso, é pedido o número de divisores de ![]() , diferentes de
, diferentes de ![]() . É importante ter atenção a isso também.
. É importante ter atenção a isso também.
Os divisores de um número natural ![]() são os números naturais que, ao dividir
são os números naturais que, ao dividir ![]() , tem como resto da divisão zero. Para encontrar os divisores de um número devemos encontrar a sua decomposição por fatores primos. No caso em questão já é dito que
, tem como resto da divisão zero. Para encontrar os divisores de um número devemos encontrar a sua decomposição por fatores primos. No caso em questão já é dito que ![]() pode ser decomposto pelos fatores
pode ser decomposto pelos fatores ![]() ,
, ![]() e
e ![]() . Supondo
. Supondo ![]() , então
, então ![]() pode ser dividido por
pode ser dividido por ![]() ,
, ![]() vezes, por
vezes, por ![]() ,
, ![]() vezes e por
vezes e por ![]() ,
, ![]() vezes. Além disso,
vezes. Além disso, ![]() pode ser dividido também por
pode ser dividido também por ![]() . Considere, por exemplo, que
. Considere, por exemplo, que ![]() ,
, ![]() e
e ![]() Neste caso, quantos números poderiam dividir
Neste caso, quantos números poderiam dividir ![]() ? É fácil ver que os números 1, 2, 4, 8 (
? É fácil ver que os números 1, 2, 4, 8 (![]() ,
, ![]() ,
, ![]() e
e ![]() ), são divisores. Considerando os fatores
), são divisores. Considerando os fatores ![]() e
e ![]() , temos também 1, 5, 25 (
, temos também 1, 5, 25 (![]() ,
, ![]() ,
, ![]() ), e 1, 7 (
), e 1, 7 (![]() ,
, ![]() ) como divisores. Além desses números, qualquer multiplicação de um número do conjunto
) como divisores. Além desses números, qualquer multiplicação de um número do conjunto ![]() com um número do conjunto
com um número do conjunto ![]() e com um número do conjunto
e com um número do conjunto ![]() , é também um divisor. Logo, neste exemplo, teremos
, é também um divisor. Logo, neste exemplo, teremos ![]() divisores de
divisores de ![]() ao todo.
ao todo.
Generalizando, teremos ![]() divisores. Como são pedidos os divisores diferentes de
divisores. Como são pedidos os divisores diferentes de ![]() , então a resposta é a letra E,
, então a resposta é a letra E, ![]() . Note que no exemplo, como
. Note que no exemplo, como ![]() não é múltiplo de 7, então
não é múltiplo de 7, então ![]() não é divisor de
não é divisor de ![]() e
e ![]() , mas isso não tem importância no resultado pois a fórmula obtida no final permite que haja expoentes zero.
, mas isso não tem importância no resultado pois a fórmula obtida no final permite que haja expoentes zero.
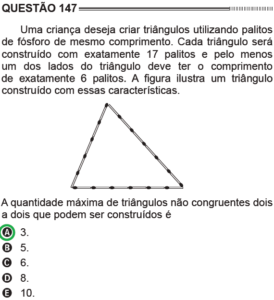
Questão 147 Caderno Azul
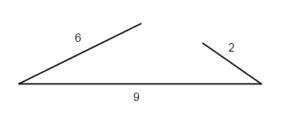
Antes de mais nada, é preciso saber o que são triângulos congruentes. Dois triângulos são ditos congruentes quando cada um dos lados de um triângulo tem comprimento igual a um dos lados do outro triângulo e vice-versa (consequentemente, os triângulos têm também ângulos iguais). Por exemplo, para um triângulo ser congruente ao triângulo apresentado na figura do enunciado, basta que tenha qualquer um dos lados formado com 5 palitos, e os outros dois 6 palitos, de forma que é possível após uma rotação do novo triângulo formado, colocá-lo exatamente sobre o outro. O que é pedido então é saber quantos triângulos que não são congruentes podem ser criados com os 17 palitos, mantendo um dos lados com 6 palitos. Esse problema é resolvido utilizando a desigualdade triangular, ou seja, não é possível que em um triângulo um dos lados seja maior ou igual que a soma dos outros dois, simplesmente porque se isso for verdade não há como fechar um triângulo. Para ver isso suponha que um dos lados seja formado com 6 palitos e os outros dois sejam formados com 9 e 2 palitos. Note que ![]() . Se tentarmos desenhar um triângulo com esses lados, teríamos:
. Se tentarmos desenhar um triângulo com esses lados, teríamos:
Observe que não há como fechar o triângulo. Mesmo que aproximemos ao máximo os lados de dimensão 6 palitos e 2 palitos (o que os colocaria sobre o segmento de reta feito com os 9 palitos), vai faltar um palito para que as duas pontas se encontrem. Logo, para resolver o problema basta encontrar as combinações de palitos que satisfazem a desigualdade triangular, mantendo um dos lados com 6 palitos e a soma dos outros dois lados igual a 11 palitos. Podemos ver que os triângulos com lados:
![]()
![]()
![]()
resolvem. Qualquer outra tentativa satisfazendo a desigualdade triangular levará a um triângulo congruente com um desses três. Logo, a resposta é a letra A.
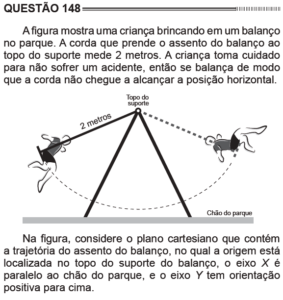
Questão 148 Caderno Azul
Note que a trajetória que a criança descreve é parte de uma circunferência de raio 2 com centro na origem que foi definida como o topo do suporte. A equação da circunferência é (fazendo ![]() ):
):
![]()
No caso em questão ![]() e, portanto,
e, portanto,
![]()
Logo, a resposta certa pode ser D ou E. Para ver que é a D, basta notar que como a origem está no topo do balanço, então ![]() é negativo para todo o movimento da criança.
é negativo para todo o movimento da criança.
Questão 149 Caderno Azul
Essa é fácil. Note que há 5 portões de entrada, sendo que cada portão tem 4 catracas. Logo, ao todo, são 20 catracas. Passará em cada catraca uma pessoa a cada 2 segundos. Logo, considerando as 20 catracas entrarão no estádio 20 pessoas a cada 2 segundos, o que dá uma taxa de 10 pessoas por segundo. Assim, as 45000 pessoas passarão pelas catracas em:
![]()
Note que 1 hora tem ![]() segundos. Logo, a resposta é maior que uma hora e certamente inferior a 5 ou seis horas. Essa não precisa nem completar a conta. É obviamente a letra B. Mas para quem quiser saber como é a conta basta fazer
segundos. Logo, a resposta é maior que uma hora e certamente inferior a 5 ou seis horas. Essa não precisa nem completar a conta. É obviamente a letra B. Mas para quem quiser saber como é a conta basta fazer ![]() e dividir 900 por 60 para saber quantos minutos 900 segundos representam. A conta vai dar 15 minutos. Logo, a resposta será 1 hora e 15 minutos.
e dividir 900 por 60 para saber quantos minutos 900 segundos representam. A conta vai dar 15 minutos. Logo, a resposta será 1 hora e 15 minutos.
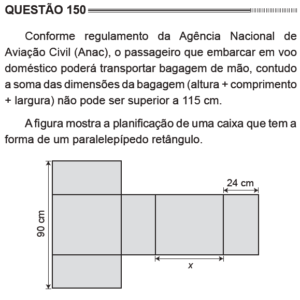
Questão 150 Caderno Azul
Essa é só ver como uma caixa é planificada. Note que os 24cm são na verdade a altura da caixa. Portanto, ela tem de largura ![]() . Como a soma de todas as dimensões tem que ser
. Como a soma de todas as dimensões tem que ser ![]() , então
, então ![]() .
.